home

contents Mathematics

previous :  counting in a different way

next :  how to travel from one number toward another?

Let's go back from zero
 

We shall not demonstrate that Cantor made a mistake in his logical argument, when approaching infinity and reaching it. We shall try to demonstrate he took the wrong way when starting. Cantor asks us to start by lining up all irrational numbers. In fact, all irrational numbers cannot possibly be lined up at the same time on the same line.

Since Cantor precisely, mathematicians have a concept called 'the real straight line' on which they line up all real numbers, according to their size [note: we recall that real numbers are made of rational numbers and irrational numbers.]
We shall try to demonstrate, even beyond irrational real numbers, that a real straight line is an impossible freak. That there is no straight line on which we could line up all real numbers at the same time.

To demonstrate this, we have to go back to the source, that is, to the way numbers are produced according to the set theory.
Let us begin with whole numbers.
 
 

In set theory to produce whole numbers we begin by making a statement: we declare that not a single thing can be the opposite of itself. For instance, that not a single thing can be positive and negative at the same time, here and not here at the same time, etc. This statement accomplished, we make a packet with all the things which are contradictory to themselves. This packet contains nothing. Then, we call it 'the empty set'. Then, we state that this empty set corresponds to digit 'zero'. Digit zero, is used to remember that we made a packet whose name is 'empty set'. This label is not put on the empty set itself. The label of the empty set, that is to say its name, is 'empty set'. Zero, is the label which corresponds to the very operation of putting it in a packet, of labeling empty set, of acknowledging its existence. Zero is used as a label --  as a name --  to designate this act. So, zero is the recording of what we have when we have nothing. So, zero points out that we have one empty set. 'One' empty set? But this is not nothing! This is 'one' thing. Let's put quickly a label on the recording we have made there is 'one' empty set. Let's call it digit '1'. So, we have made the recording of a set which contain nothing, and the recording of a set which contains 1 thing (the empty set). That makes 2 things. Quick, a label to remember this new recording: digit '2'. It then makes 3 things: digit '3', etc. Of course, till infinity.

When generating numbers in such a way, by putting in one set, things which are the opposite of themselves, we notice two important facts.
        - first, we find nowhere in the numbers we produce thus, anything which looks like a decimal number, a fractional number or an irrational number. We always fall down exactly on whole numbers, never between two of them.
        - secondly, we notice that we cannot make the recording of empty set, without recording its existence at the same time, therefore that there is a set which contains nothing, therefore that there is one set, therefore that there is some 'nothing' and some 1, therefore 2 things, therefore some 'nothing', some 1 and some 2, therefore 3 things, and so on.
So, making 0, 1, 2, 3, 4, etc. to infinity does not amount to move forward progressively as on a straight line, with small repeated leaps occurring the ones after the others, and making notches in the line, each separated from the others. On the opposite, it is unrolling in one go all the numbers till infinity while we are still doing 0.
All whole numbers are thus contained in zero, condensed in zero. Even infinity.

Of course, afterwards, that is after they have been generated, nothing prevents us from lining up all positive whole numbers on a straight line, which starts in 0 and goes till infinity. But that's storage, a spreading. Nothing to do with the dynamic creation of whole numbers. Nothing to do with the fact that they exist, that we can produce them.
 
 
 
 

Now that we have whole numbers, let's see fractional numbers such as .1 or .23489421. All whole numbers being condensed in 0, there is no path between 0 and 1. There is no path that we could graduate by putting the label of a decimal number on every interval met between 0 and 1. If we want to graduate something, without being able to circulate on this thing, doing marks along such a path, the only way we have is to deform this thing and to graduate the intensity of the deformation. That is the way we shall generate fractional numbers and irrational numbers: graduating the intensity of a deformation, in a manner that the complete absence of deformation will be graded 0, and the maximum possible deformation will be graded 1.

You will say that this procedure is not in set theory.
But we did warn that we would suggest a change with the idea we have of numbers.
Besides, what we shall now do, is not really to suggest a new way of counting but to realize what we really do when we pick up a decimal number.
In the same way as Molière's hero Mr. Jourdain could write and speak in prose without being aware of it, surely we do 'something' when we 'pick up' a decimal number. If set theory is right when it says that we generate all whole numbers in one go by designating the existence of 0, itself designating the existence of empty set, then we are forced to admit that what we do without being aware of it when picking up a decimal number, cannot be a path: it can only be a deformation.

How do we do?
Let us pick up a decimal number at random. For example .340238911352. We notice several inescapable facts:

       1/     First, we put a decimal point. That is to say, we put a label of a special type, which is used to remember that what is left and what is right of this sign, must not be mixed.

       2/     Then we put several decimal digits that are as many labels as things we want to remember. In this case, we used 12 decimal digits. We used 12 digits because we needed them. If we could have used fewer, we would have done so. On the other hand, we know that we can add as many digits as we want behind these 12 digits: that will not change the number provided we only add digits 0.

       3/     The order of the digits is also significant. Number .129 is in no way, the same as number .912. Then, there is also something we want to remember, which is contained in the order in which we line up decimal digits.

       4/     Last but not least: we only use 10 different labels, which are enough to create and designate all decimal numbers: the labels 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Then what we want, at every decimal digit, is to keep the trace of something which can only take 10 regularly graduated values. By the way, we can notice that we could have proceeded differently. Instead of using the first 10 whole numbers, we could have used letters of alphabet, or any small drawing as well. The fact we use the first 10 whole numbers to name decimal digits, has nothing to do with the fact that they are numbers. It's only that we remember the order in which they are lined up more easily, than for instance the order of a star, a four-leaf clover, an ace, etc.
Also, we are not obliged to use 10 graduations. This number is only valid for numbers in '10 base'. We could as well have used numbers with 16 base or more. In fact, the bigger the number of labels, the fewer decimal digits will be needed, for the range of graduation covered by every label is all the thinner. Computing commonly uses this property, when using for instance all the letters of the alphabet, and even all other keyboard signs instead of numbers. This allows every number, made with successive choices in that multitude of signs, to be composed of fewer labels than if made of successive choices in the first 10 whole numbers. In that way, they occupy less space in the memory where they are kept. Thus for instance, a number can be recorded as: 4#DF.
 
 
 

Now that we have listed all the sorts of traces which we try to remember when we name a decimal number, let us describe step by step, how we manage to produce such a number. First, we pick up a whole number, from 0 toward positive infinity or from 0 toward negative infinity. And we leave it untouched, without deformation. Then, behind it, we put a decimal point indicating that from now on we shall begin to do something of a different nature from the whole number already placed. Something we could not reduce in that number, we could not name with it. After the decimal point, we list intensities of deformations, one after the other. We begin by making a first deformation, whose intensity will be marked out with a 1st label behind the decimal point. In our system in 10 base, we can use 10 intensity values. Then, there can only be 2 possibilities: either the number we try to indicate precisely corresponds to one of these 10 possible values of deformation, either it doesn't. It cannot be 'between' 2 values, for these values do not correspond to coordinates of graduation marked on a line, but correspond to intensities of deformation: as there is no notion of distance or notion of path in the relation of these 2 values, there cannot be a notion of 'between'. If we do not have exactly our number after a first deformation, we shall keep as a reminder, the label corresponding to the intensity of the last deformation we have found before we had missed the number. That is not 'the nearest' to the number we search, for there is no distance: that is 'the latest', before we notice the failure. So, a 1st deformation, jumping by rigid steps of intensity from 0 to 9, was not enough to get the number. Then we start again with a 2nd deformation. Its reminder will be kept in the same way, by designating the instant the number is failed with the intensity of the deformation measured at that moment. And so on until we get the exact number we have been searching. When we have it, if we want, we can put behind as many 0 as we wish. This will only serve to remember that all the deformations we are now making have an intensity equal to zero. But it is no use bothering to do so and we have better not to do this: if we refrain from putting these 0, that will point out that we have stopped deforming the number. If we want an irrational number, we shall proceed as with any decimal number. We just have to continue infinitely to make a deformation following another, and to mark the failure every time with a label.

So, here comes the question again: can we put these fractional and irrational numbers we can produce in that way, all on the same straight line? And preferably on the same straight line as all whole numbers?
This time the answer is no! Definitely no!
For, if we want to keep all the data which were useful to get a decimal number, we have to keep track of all these successive deformations, and of their order of occurrence.

If we want to keep all these data in a "spatial" way, that is in a graph, the least we can do, is to spread this succession of deformations the ones beside the others, without changing their order, nor their number, nor the intensity value noticed at every failure.
If we lose only one of these data, we lose what distinguishes one number from another, we wrongly mix two different numbers, and we lose the number we wanted to represent in a space.

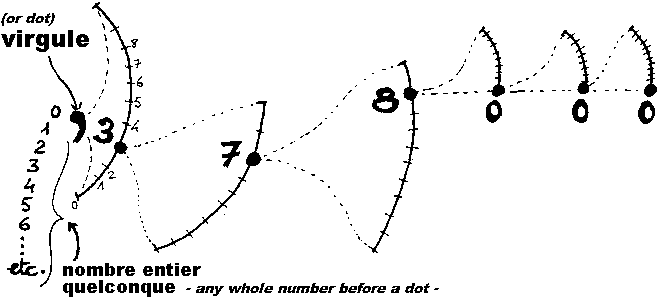
If we draw a diagram keeping all these data, we can see clearly that a decimal number, to be represented, requires a space with a minimum of 2 dimensions: then, that's a surface, not a straight line.

If we draw together, on such an infinite surface, all decimal numbers, the surface will then be paved with junction knots. We shall not be able to remove them, or to cut them so as to 'give way to' the more remote numbers and to bring all of them back on the same straight line as those we had begun lining up.
You can also understand this impossibility, in the following way: one point on a straight line marks one position. This marking can only keep one datum, that is the distance to the origin 0 of the straight line. But to keep memory of the operations which are used to differentiate one decimal number from another, we have to retain several data: how many deformations, in what order, and what intensity for every deformation. We cannot use a system with one datum only to locate a decimal number requiring several of them. Unless we agree to lose a considerable part, of what is used to differentiate one number from another.
Of course, if for convenience we agree to lose data about numbers to put them on the same straight line, when doing demonstrations about their properties we have to refrain from using this way of storage which massacres them. Yet, that's what Cantor asks us to do, when beginning asking us: 'put all the irrational numbers in the same column'. If we extend until infinity, a reasoning which starts massacring numbers, making them lose more than half their properties, we must not be stunned if we get freaks when reaching infinity. Nor be worried.

Even whole numbers cannot be correctly depicted all and together, by a straight line. For there are more data in the infinite series of whole numbers than there are in the infinite series of the points on a straight line. This extra datum is that whole numbers are at the same time all mixed up with zero and all having a gap of '+ 1' between one another. The points of a straight line, are 'only' differentiated by a gap between them. They are not 'also', gathered in the same point.
Thus, the data contained in the set of whole numbers are not of the same type as those contained in the set of the points of a straight line. For that reason, you cannot use the properties of one to deduce the properties of the other.
 
 

home

Math

top

next :   how to travel from one number toward another?

author