home

contents Mathematics

previous :    Mandelbrot fractal dimensions to the rescue

next :    continuity of deformations in space

The difference between fractal and space dimensions
 
 

Now we shall see the crucial point, where we have to think of the notion of fractal dimensions in the newest way. In a space of coordinates, the dimension 1 corresponds to curves, 2 corresponds to surfaces, and 3 corresponds to volumes. Usually, fractal dimensions are thought in the same system, and considered as 'parts' of space dimensions:

     -  a dimension between 0 and 1, is supposed to correspond to the capacity of a set of points to partly fill a line, without achieving it completely, out of having the whole value 1 which is needed;
     -  a dimension between 1 and 2, is supposed to correspond to the capacity of a line to partly fill a plane, without achieving it completely, out of having the whole value 2 which is needed;
     -  a dimension between 2 and 3, is supposed to correspond to the capacity of a surface to partly fill a volume, without achieving it completely, out of having the whole value 3 which is needed.
 
 

To think in this way, is to think with old reflexes.

It's to bridle fractal dimensions in thinking them still as coordinate dimensions. The data born by fractal dimensions are richer, and this richness is revealed, only if we completely give up this system of location in space. Fractal dimensions correspond to another system of relations, for they are deformation dimensions, not coordinate dimensions.
Of course, every phenomenon evolves in space. And here, we shall not say that space-time where the universe evolves, holds more than 4 dimensions, 3 of space and 1 of time. But every phenomenon that evolves in space-time, can basically be seen as the interaction of a random number of deformations, each of them being measured with a fractal dimension.
 
 
 

A fractal dimension holds 2 parts: a whole number, then, after a dot, a decimal number. We have already suggested the signification of these two parts. We now see this question again, in a more precise and a more complete way, beginning with the whole number.

We make the hypothesis that the 1st digit of a fractal dimension, its whole number, has nothing to do with a notion of space size. We suggest its explanation as follow:
 
 

      "0" :  We gave an example [to see    this example again] of a contrast value, measured with spots on a white sheet, then, in a 2D space. Instead of 2D spots, we could have taken 3D black bubbles in a 3D white volume: the contrast ratio measuring the ratio between the volume of the bubbles and the whole space, would always have been less than 1.
Therefore, a fractal value smaller than 1, whose 1st digit is consequently 0, has nothing to do with the incapacity to completely fill a line 1D.
Digit 0 only indicates that the phenomenon implies no displacement in space. The deformation of the whiteness of a line, of a page, or of a volume, implies for itself the motion of no single point at all, but it implies the appearance or the disappearance of an infinite number of points.

Then, the dimensions with 0 as whole value are specially convenient for the measurement of mutations: what is uncolored becomes colored, what is young becomes old, what is inert becomes lively, what is healthy becomes sick, etc.
But we cannot see a move explaining the turning of a young person into an old one: before becoming old, and old person is nowhere among the old persons. Then one day he or she appears with this property, coming from nowhere, and one day he or she dies, disappearing with this property from the old persons.
 
 

      "1" :  When we gave some examples of fractal curves (for instance     Van Kock's snowflake curve), we saw that when the deformation implies a displacement in space, then the whole value of the fractal dimension is 1.

This type of dimension is uniquely convenient to describe the moving of a body.
It is not convenient to describe or to predict the possible changes of its property while moving, which fits to the dimension 0 we just saw.
Nor is it convenient to describe its possible deformations while moving, which fits to the dimension 2 we see now.
 

      "2" :  We have already suggested that the whole value 2 of the Peano curve [see below its representation] has to do with the deformation of a surface on itself. More generally we suggest now that the whole value 2 in a dimension has to do with the deformation of a body on itself. With this term we mean the coordinated internal displacement of all its points, all exchanging one another, without the global displacement of the body in space.

In the section "science" of the french site, we suggest that a particle of matter is the result of a very complex movement that works in a close loop, which is exactly a case of internal deformation. So, all what is related to the stability of matter particles and their internal coherence is specially concerned by this type of dimension.
Laurent Nottale who tried to combine quantum mechanics of elementary particles with fractal calculation, end up with the same conclusion.
We translate an extract of one of its article ['L'espace-temps fractal' - Pour la Science - September 1995];
'The two dimension is, precisely, those of the fractal trajectory calculated from Heisenberg's uncertainty relations'
 
 
 
 

To sum up, our hypothesis is that if the fractal dimension is 0,x then it's a contrast value, if the fractal dimension is 1,x then it's the value of a trajectory, and if the fractal dimension is 2,x then it's the value of an internal deformation. But here too, like what we saw for the value 0, we emphasize that the values 1 or 2 have nothing to do with the number of the dimensions of the space where the phenomenon occurs.       - so, a path (deformation dimension: 1.x) can as well remain fixed to a curve, than evolve on a surface, or spread in the whole space;       - and the deformation of a body on itself (deformation dimension: 2.x) can as well be that of a filiform body, than that of a surface, or that of a 3D body.

 

Then, if the whole number gives no information about the evolution of the deformation in space, decimal digits have to do.
In that respect we make the hypothesis that the decimal value of a fractal dimension indicates how the intensity of the deformation varies according to space directions.

If the deformation is restricted to a line or to a surface, the decimal series will do in such a way that the deformation value will be null in all the forbidden directions.

 

Another significant point, which results from the incommensurability between whole part, and decimal part of a fractal dimension: the whole part has nothing to do with the intensity of the deformation.

For example, a 2.1 dimension is in any way a more intense deformation than a 1.1 dimension. This is fundamental for the comparison of fractal dimensions the ones with the others: for example, a dimension 1.999 . . . . and so on, is not a dimension very close to dimension 2. Rather, they are bound to be very far away from each other: one is an extremely tortuous path that can occur even in a 3D space, whereas the other can concern the deformation of a surface only, even of a curve only.    [see the example below]

 

But here is a new important subtlety: we can think of a dimension with a value 2, in two completely distinct ways.
Either we say that it's a dimension 2.0, that is, for example, the regular deformation of a surface on itself, such as made with the evolution of a 'Peano curve'.

==>

==>

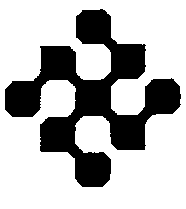etc

a Peano 'curve' regularly paves a surface, every step making a more tortuous division between its two interlocked halves:
its fractal dimension is 2.0

Either we say that it's the limit at infinity to a dimension 1.99999 (with 9 till infinity). That is, a path which is subjected to the maximum roundabouts that a path can be subjected to, roundabouts that are systematically and completely random.
This has nothing to do with a surface. This, is precisely the fractal value of what is called the 'Brownian movement', the movement of gas molecules, moving absolutely randomly in all space directions. Then, with maximum irregularity in their path. Doing this, they move within a 3 D volume, not on a 2 D surface.
 

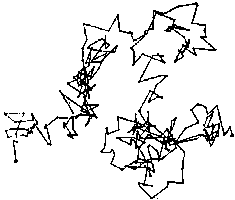a sample of Brownian movement: its fractal dimension is 2 but its signification would be 1.9999999 till infinity

 

We can also consider mixing space dimensions and fractal dimensions.
Thus, a Menger sponge [to see     this figure again], has a fractal value Log 20 / Log 3, close to 2.7268.
The whole part '2' would not correspond in this case with the information to the type of the deformation. Its type corresponds to the dimension 0, for the generation of this volume is similar to that of a Cantor dust.
The value 2.7268 corresponds to the evolution of the surface separating empty parts and full parts of the volume. It has to do with the conversion in terms of surface (then the value 2D) of a process of generation with dimension 0,x.
 
 
 

In the end, if fractal dimensions are more general than space dimensions, it implies that space dimensions are only fractal dimensions with special values. Let's calculate their value: On the axes of measurement of the Euclidean space, the coordinates follow straight paths. Being paths, they deserve 1 as whole fractal value. As these paths do remain straight ones and are subjected to none deformation in any direction, they deserve the decimal value 0. In short, fractal dimensions are not special and partial space dimensions, on the opposite space dimensions are only a special and limited case of fractal dimensions, with the very special value 1.0.

 
 

home

Math

top

next :      continuity of deformations in space

author