home
contents Mathematics
birth of a dimension
chains of dimensions
home |
contents Mathematics |
previous
: birth of a dimension |
next
: chains of dimensions |
| direct to all other pages of the section ----> | 00 | 01 | 02 | 03 | 10 | 11 | 12 | 20 | 21 | 30 | 31 | 32 | 33 | 34 |
To see what's going on in the 4th dimension
How many simultaneous dimensions
can we represent and read in a continuous way? Three for the three dimensions
of space, and one fore time dimension, then it makes four.
To get these 4 dimensions we make
a frame of 3 dimensions of coordinates, and in this frame we represent
the location of a moving body at various times. It's a usual 3 D + T diagram:
in it we 'hold back' the successive locations of the body in its move,
the ones besides the others, which enables us to represent the 4th dimension,
time dimension.
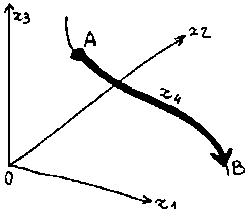 evolution
of the body from A to B in 4 simultaneous dimensions evolution
of the body from A to B in 4 simultaneous dimensions
It's the continuous line AB that represents the continuity of the 4th dimension, generally use to represent time dimension |
We can
therefore consider using such a diagram with 3 D + 1 dimensions to represent
the 4 dimensions of a 4 D + T deformation, provided we give up the idea
of representing simultaneously its time dimension.
In the case of a phenomenon that
gains a 4th self-similarity dimension, that's what is happening in a continuous
way in this dimension of self-similarity that can be represented instead
of what is happening in a continuous way in time dimension.
Now, we understand that it's
very precisely this, that the Robert Shaw's team got
in the diagram which 'faked' the 1 D series of the chaotic phase of the
dripping tap [to see again ![]() this diagram].
this diagram].
Every dimension of the 3 D diagram
(abscissa, ordinate, height) holds the values of all measured time intervals,
but as these values are shifted of one step between each dimension, the
continuity that appears on the 4th dimension of the graph is what is 'transverse'
of all the measured time intervals. And what is transverse to time dimension
where they were produced, and what is also transverse to every deformation
that produced them, that's precisely the interference of the deformations,
which happens to be, in this phase of the phenomenon, self-similar.
Then, what the graph shows, is the
look of the continuous deformation of self-similarity provoked by the interference
of the 3 initial deformations of the phenomenon.
As there is only room on this
diagram for 4 continuous deformations, the self-similarity deformation
replaces time dimension there.
We have explicitly given up time dimension when gathering time intervals
in triples, for in these triples every time interval is not only confronted
with the time interval that follows it in time, but also with that which
follows the following: we then jump over the strict continuity of what
follows in time, we broke the 1 D ordering of time. As a result, on this
4 D diagram (4 deformations), a point and its following in time have no
relation of continuity, therefore no relation of proximity.
Now we are coming to the very look
of a diagram which represents a dimension of self- similarity.
When the 4th dimension of a 3 D
+ 1 D diagram represents the continuity of time dimension, its aspect is
a continuous curve: every successive point of this curve touches one another,
exactly as every successive sequence of time touches one another.
Then,
when the 4th dimension represents the dimension of self-similarity we must
expect it to look like a self-similar diagram, for in the same way as a
continuous movement has a continuous curve as 'image', a self-similar dimension
has to have a self-similar diagram as 'image'.
And this is precisely what we
got.
We cannot observe it in the case
of the attractor drawn by the Shaw team, for it's a 'blurred' diagram,
but we know that this diagram is a partial cross-section of an attractor
known as 'Rössler's attractor'.
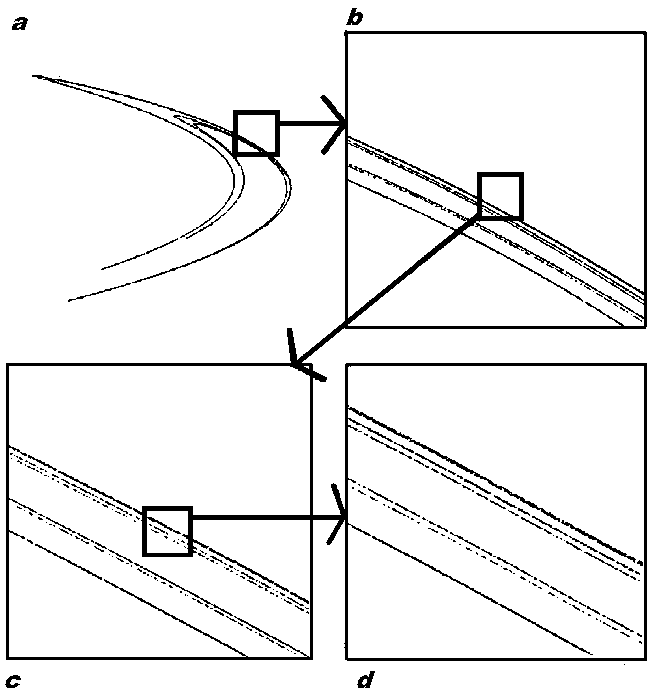
self-similarity of Hénon
attractor in all its scales
This curve is mathematically calculated, and with the help of simulation calculation we can examine it as under a microscope which enlarges 1000 times. Thus, the diagram show in a an overall view of the curve which represents the successive positions of the same start point. In b, is a 10 times enlargement of the small square of a. In c, is a 10 times enlargement of the small square of b. And finally in d, is a 10 times enlargement of the small square of c. Then in d is a 1000 times enlargement of a detail of a, which looks like the overall pattern of the central part of a. In the same time, d represents a part of c banding which is so much similar to c and b banding in their number and in their rhythm of succession (2 very closed lines on the outer side, then a small gap, then 2 relatively closed lines, then a medium gap, then 2 extremely closed lines on the inner side), that it is impossible to differentiate a view and a 10 times smaller view or a 100 times smaller view, except for the radius of the curve which slowly change from one diagram to another. It's hard to believe that the 4 double-lines in the 'd' diagram are nothing but the enlargement of the 2 external double-lines in the 'c' diagram, and when we understand this, we expect that, provided the calculation unables us to enlarge 10 times more the diagram, we should see the same pattern in 4 double-lines in the enlargement of the external lines of d. Whatever the scale, the detail in the detail is absolutely the same as the detail in the detail in the detail, etc. [note: simulations of Hénon attractor show the same self-similar structure in the sharp part of the diagram a as in the central part of a, and with the same pattern of banding. Then, these two parts are only differenciated by the radius of the curve, which is modered in the central part, and very sharp in the other] The shape in one aspect of this figure.
We have already explained the cause of this chaotic movement of the point: the dimension of time continuity has vanished to make room for the dimension of self-similarity dimension, for the diagram does not have enough dimensions to simultaneously represent these two dimensions. |
| Now all is clear as
it seems: we said that
a self-similar dimension had to surge and to drive out time dimension for
in the diagram there is no room for the two dimension at the same time,
and we did find on the diagram that time continuity is broken and replaced
by another type of continuity, that of the similarity in all scales of
the pattern.
And yet, there is always and intriguing mystery. |
| Besides, there are attractors
that do not look like lines or banding.
For example, the diagram of 'logistic mapping'. Here we give this diagram
in several scales: points group together only vaguely, and we can only
call 'shade' these more dense areas that don't have a linear pattern.
|
So, strange attractors spread on
surfaces with variable density, not on lines.
This is the remaining mystery, for
this is not directly obvious.
In the
same way as the continuity of a movement in time dimension is represented
by a continuous curve, we could have expected that the continuity of self-similarity
dimension would be represented by a continuous self-similar curve.
For self-similar
curves do exist:
we have seen such a curve already.
For instance, strange attractor
could be something like the von Kock's snowflake curve [to
see it ![]() again],
rather than being something like the Peano's curve/surface [to
see it
again],
rather than being something like the Peano's curve/surface [to
see it ![]() again].
again].
We have understood the
reason why a point makes random jumps in time dimension,
but why does it make
its jumps on a surface rather than on a line?
home |
Math |
top |
next
: |
author |