home

contents Mathematics

previous :  Ian Stewart drips his tap

next :  to see what's going on in the 4th dimension

Birth of a dimension

We have begun to speak about the interference between the 3 deformation causes that produce drops.
Our assumption, about the cause of the onset of chaos, concerns a particular characteristic that this interference takes, at a particular moment.
Ian Stewart explains in his book 'Does God Play Dice' [to see   again] that when chaos surges, there is always something in the phenomenon which becomes self-similar. Here, we assume that it's the resultant deformation, produced by the interference between the 3 initial curved deformations, which then becomes self-similar. This immediately provokes the onset of chaos.
We shall now try to explain why.
 
 

If the 3 causes provoke a combined resultant deformation which is self-similar, it means that whatever the scale we can pick up to consider the drop being formed, the interference between the 3 curved deformations (pressure, gravity and capillary tension) forms a part of interference which is in phase with the global interference. What changes is this: from now on, if we increase the pressure of the 1st deformation a little more, that supplement will be taken in a coordinate way on all the scales of liquid. As the number of scales in which a phenomenon can be cleft tends toward infinity, it means that this supplement of deformation will be divided almost infinitely. It will be split up, cut up, between all the scales of the liquid. It will lose some of its 'deforming power' proportionally, therefore it will lose it 'infinitely'. It happens that dividing infinitely amounts to reduce to zero. And what is true for the pressure deformation, will be true for the two other deformations, in the same way: suddenly each one of the three deformations will then become equal to zero. This can be summarized by telling that the self-similar character gained by the interference of the 3 curved deformations, becomes a cause of stabilization of the deformation, a cause that opposes any increase of deformation, by spreading it on infinity of scales. Therefore, self-similarity acts like a force that compels the deformation phenomenon to decrease. It 'deforms the deformation' of the phenomenon. It becomes a new cause of deformation, since, without it, the phenomenon would have had a different form.

We have just said that a cause that makes a deformation stop, has to be called 'deformation'. There's no need to be shocked, for it's strictly similar to the case of a cause that opposes a moving body, a force of friction for example. It's called 'force', like the opposite cause which tends to increase the move of the body.
Here, what opposes the change, is called 'deformation', as the opposite cause which tends to increase the change.

Then, self-similarity is a cause of deformation, but more than that it is an autonomous cause of deformation, a cause distinct from the first 3 ones, for the first 3 act to increase the deformation, and the new one acts to limit it.
Although it is the result of their interference, it has nothing to do with the 'addition' of these 3 causes.
Previously we gave a diagram [to see   this diagram again] which indicates how the vectorial calculation of forces could lead to a wrong result when confronted to the interferences of the forces. Probably it's right here -- where the explanation of what's going on is all in the interference's characteristic -- that this traditional vectorial representation is the more disabling: it misses all the process, it makes us blind on what's going on.
 
 

It's not the first time that we have to consider that the self-similar character of a phenomenon acts as a force. As a matter of fact, Pierre Gilles de Gennes, in his article 'la matière ultradivisée' [L'Ordre du Chaos - Bibliothèque Pour la Science - diffusion Belin], gave another example of this. He considered paint grains, each of them surrounded with a polymeric aureole. The chains of these polymers put themselves in a mesh which is self-similar on all scales. Then Pierre Gilles de Gennes concludes that this self-similarity of the patterns, when it tries to reproduce itself also in the interference of all aureoles of all the grains, then acts like a force. A force that repels grains the ones from the others, and prevents them from gathering and piling up as they would have done without aureoles. the self-similar structure of a diffuse polymeric halo round a grain, according of P.G. de Gennes

 

To return to our dripping tap, we have then, in the evolution of the interference of the 3 forces which cause the deformations, a moment when this interference gains a self-similarity property, that changes it in a force:
      - in a force distinct and autonomous of the first 3 forces for it does not act as they do;
      - in a new cause of deformation, that acts in all the volume, and in a similar way on all its scales.
Then we have the properties needed, for a cause of deformation to be called 'dimension':it deforms, for its own purpose, in all directions, and in the same way on all scales. That's a self-similar dimension of curved deformation. Therefore, that's a 'fractal dimension'.

So, we began with a tap dripping in a 3 D space (3 dimensions of space), under the prompting of a 3 D phenomenon (3 dimensions of deformation). Suddenly, the tap which goes on dripping in a 3 D space, is influenced by a 4 D phenomenon (4 dimensions of deformations: the first 3, and the dimension of self-similar interference).  Therefore, the immediate description of what's happening is that space dimensions are 'overflown' by the number of dimensions of the phenomenon. Space dimensions cannot contain in a continuous way all the dimensions of the phenomenon, for self-similarity gives it a dimension in excess. But nothing can prevent the phenomenon from holding more dimensions than its receptacle. Having more dimensions than space where it evolves doesn't disturb the phenomenon. The consequence is that nothing changes for the phenomenon: it goes on being perfectly determined by the interference of its fractal deformation dimensions, which are now 4. There is a change for us only. For we can only see 3 deformation dimensions at the same time, developing in a continuous way in the 3 D space. Necessarily the 4th deformation dimension doesn't correspond any more to any link of proximity, with any visible continuity in 3 D space. For us, it's apparent chaos. Visibly, parts of the phenomenon are scattered, with no continuous link between each other. But in the reality of the causes acting in the phenomenon, they are continuously linked the one with each other in all the 4 dimensions.

 
 

To give an equivalent of what 'to be linked in reality but not visibly' means, you can imagine that we are a 1 D creature (a straight line for example), and that we try to see a square (2 D reality) going through us.

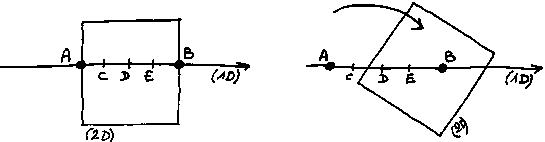
As a 1 D creature, all what we can see and understand of the square, are points A and B where it pierces us. For us, these 2 points are perfectly separated, discontinuous. There is infinity of points C, D, E, F, and so on, that separate them and prevent them from being linked. We have no way to conceive that, in reality, these 2 points are continuously linked on a square figure. Because for us, in our 1 D universe, a square does not exist, does not mean anything. For us, all that is continuous between A and B, necessarily goes through C, D, and so on.

If the square starts moving, for instance starts to slide along our straight line/universe, we shall be unable to grasp any connection between the fact that the square is leaving A, and the fact that it leaves B simultaneously. For us, there will be 2 displacements whose causes seem independent from each other. In addition, if the square starts rotating while sliding, the rhythm of displacement of B will consequently vary in a different way from A. The connection between the evolution of these 2 rhythms will seem completely random to us, especially when the crossing of a summit will change the direction of the movement.

We shall say it is chaos, and if we are smart enough to notice some occult determinism in it, we shall say this is deterministic chaos. But this would appear to us in that way, only because the cause of the evolution (the motion of a pivoting square) has one dimension in excess to be continuously grasped in our 1 D universe.

When self-similarity changes a 3 D + T (time) phenomenon, in a 4 D + T phenomenon, it's exactly the same thing for us, who are in a 3 D + T universe. We are unable to see, and to grasp, 'what links' continuously what is happening in a 4th dimension.

Now we can suggest an answer to the question 'where is the order of deterministic chaos hiding?': it's not hiding, it only evolves in a 4th dimension for which we are blind, for we can see continuously only 3 simultaneous dimensions in 3 D space.
But we must be careful to consider that it doesn't evolve in a 4th space dimension, which doesn't exist. It evolves in a 4th deformation dimension. What makes chaos for us, is that space has only 3 dimensions, which is not enough to let the continuity of 4 deformation dimensions appear at the same time.
 
 
 
 

home

Math

top

next :    to see what's going on in the 4th dimension

author