fractal dimensions of Mandelbrot and chaos theory - 14

home

contents Mathematics

previous :

to see what's going on in the 4th dimension

direct to all other pages of the section ---->

Chains of dimensions

When a line is being drawn, as the time passes by its points jump from one position to another position of this line. In a strange attractor, points do not jump anymore on a line but jump on a surface.
So, we only have to acknowledge the evidence: a strange attractor does not represent the evolution of a line, but that of a surface.

We shall make the hypothesis, that this mutation of the diagram along with the increase of the number of its dimensions (a 1D line being replaced by a 2D surface) would have link with the mutation of the represented fractal dimension: a line would represent a fractal dimension '1', and a surface would represent a fractal dimension '2'.
But we cannot understand the meaning of this mutation if we only consider the functioning of a strange attractor, and we now have to suggest a general hypothesis on the chain of all types of dimensions. To present our hypothesis, we sum it up in a tabular form.

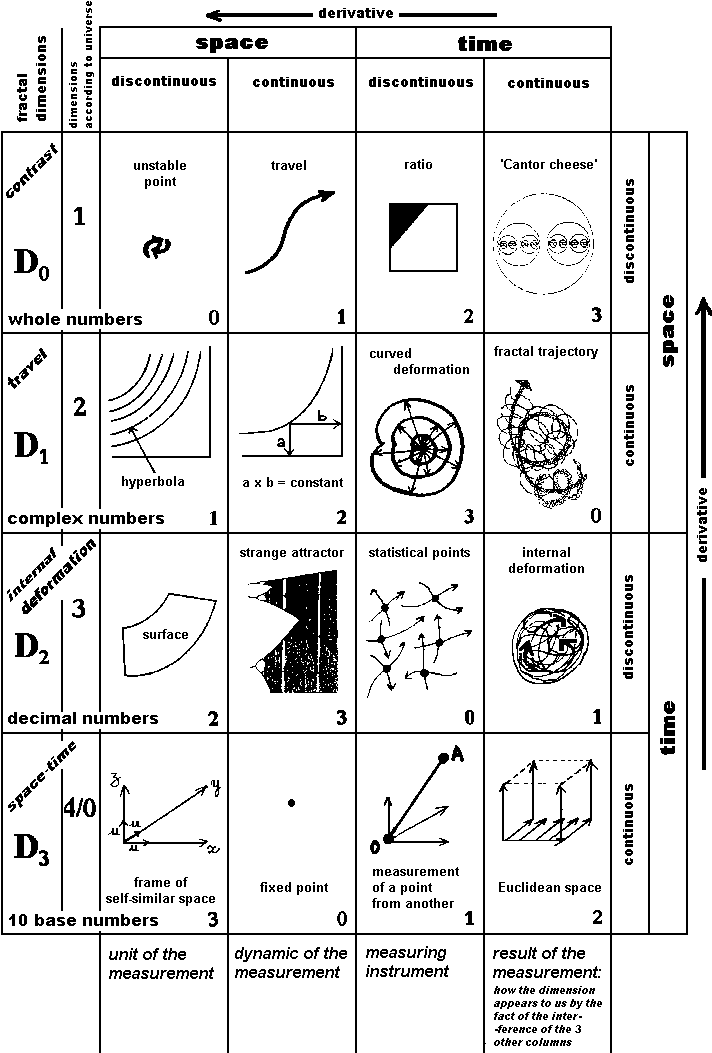
Every horizontal line corresponds to fractal dimension, from 0 to 3.

- in the 1^st line, we find the fractal dimension whose whole part is 0. We said it's specially convenient for the measurement of a contrast [to see this again].
The first two squares of this line show a functioning which is similar to what we described for the generating process of whole numbers: the instability of 0, whose vibration unwind in one go all whole numbers till infinity [to see again the chapter "Lets' go back from zero"].
Then, we will say this '0' fractal dimension is that of whole numbers.

- in the 2^nd line, we find the fractal dimension whose whole part is 1. We said it's specially convenient for the measurement of the motion of a body [to see this again].
This dimension works by the simultaneous measurement of two values. As this characteristic is also that of complex numbers, we will say this '1' fractal dimension is that of complex numbers.

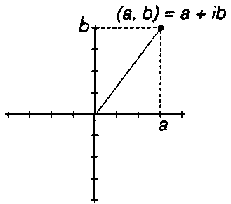complex numbers can be written down
in the form a + ib
(where i is the square root of -1)
or be represented by a couple of numbers

- in the 3^rd line, we find the fractal dimension whose whole part is 2. We said it's specially convenient for the measurement of the deformation of a body on itself [to see this again].
In the chapter "Let's go back from zero" [to see this chapter again], we explained why decimal numbers need a '2' dimension to be produced and recorded. Then we will say this '2' fractal dimension is that of decimal numbers.

     - in the 4^th line, we find the fractal dimension whose whole part is 3. Until now we did not suggest a meaning for this type of dimension.
Now, we suggest that this dimension is that of usual coordinates in a space-time diagram.
The '3' dimension being specialized in the interference between previous dimensions, we propose to consider it to be the dimension that enables the combining of whole numbers with complex numbers and with decimal numbers.
As the 10 base numbers make possible to easily calculate numbers in all situations, we will say this '3' fractal dimension is that of 10 base numbers.

Then the 1st line corresponds to fractal dimensions with 0 for whole part.
As we suggest, these dimensions are to calculate contrasts.

         - in the 1st column, we find the mathematical figure that enables us to make the measurement [the caption describing the function of every column is under the table]. As a contrast can be measured by the ratio between two values, the result of this ratio is just a number, and a number can always be represented with a point on an axis. Then the 1st square is illustrated with a point, but as this point is not fixed and on the opposite can endlessly move on a curve, we say it's an 'unstable' point. It's the perpetual instability of such a point by the effect of its internal contradictions, that would make constant its move.
         - in the 2nd column, we find the dynamic used by the measurement instrument of the 1st square. As we just said, this dynamic is an unstable point, then a line. We can also say: a travel.
         - in the 3rd column is the way used to measure the dimension. What we measure is the effect provoked by the deformation, and the type of the measurement varies according to how its environment reacts to the deformation. Here, the deformation provokes a contrast, then the measurement is the measurement of a ratio.
         - in the 4th column, we find how the measured dimension organizes itself, that is finally, how the phenomenon appears to us in reality. Here we give the example of the 'Cantor cheese' we can construct as a Cantor dust [to see again    a Cantor dust], starting with a ratio that we make constant in all scales.

In every corner of every square of the table, we put a dimension value which enables to read the table in a diagonal order. This reading is thus crossed with the progress along the lines and with the progress along the columns.
We note that on every diagonal, from the left bottom to the right top, the corner dimensions are identical. This means that diagonal progress is well balanced for the reading of all squares when we go from the left top to the right bottom.

When we find the digit '3', this means that we are in the square where the self-similar character of the fractal dimension is working.
For the '0' dimension, it's then in the 4th square that this character appears, and the Cantor cheese in this square is coherent with this specific character.

When we find the digit '2', this means that we are in the square where the decimal value of the fractal dimension is working.
For the '0' dimension, it's then in the 3rd square that this character appears. It's given by the result of the measured ratio.

When we find the digit '1', this means that we are in the square where the complex function of the fractal dimension is working.
Here it's not very 'complex', for it's only a line that we find in the 2rd square.

When we find the digit '0', this means that we are in the square where the whole value of the fractal dimension is working.
Here we find it in the 1st square, with a point that is not even stabilized. Digit 0 for this square seems appropriate.

The 2nd line corresponds to fractal dimensions with 1 for whole part.
These dimensions are specially convenient to calculate the movements.

        - in its 1st square we find the state of 'what is used to make the measurement': they are hyperbolic curves. The characteristic of a hyperbola is that for all its points the product of the abscissa with the ordinate is constant. Gauss, who gave complex numbers the presentation still used by mathematicians, also showed that complex numbers are connected with the hyperbolic curvature of a space. These works led right to the notion of curvature of space by masses proposed by Einstein, whose calculation precisely uses complex numbers. It occurs that the diagonal reading of the table, as well as the reading along the lines, corresponds in this square with the dimension of complex numbers.
         - the dynamic we find in the 2nd square comes from what we just said about the particularity of a hyperbolic curve: what is here constant is not an isolated value but the product of two coordinates, one as an abscissa and the other as an ordinate. The dynamic of this dimension is then the dynamic of continuous coordination of two '0' dimensions. The decimal value of the '1' dimension will vary according to the relative size of these two '0' dimensions.
         - in the 3rd square we find the way of the synchronization in all scales (diagonal reading) and how the dimension works (reading by columns). The dimension works by a movement impulse in all directions, which we represent by an infinite number of vectors toward all possible directions, as we suggested before [to see    where we suggested this representation]. The specific shape of every 'bunch of vectors' is given by the decimal value in the previous square, and the self-similar dimension is given by the similarity of the shape of this 'bunch of vector' in all scales.
       - in the 4th square we find the way the dimension appears to us by the effect of the interference of its first 3 aspects: it appears as a move, a travel, the travel made by the body when subjected to the multiple impulses resumed in the bunch of vectors that we see in the last square. In space, a move corresponds to a whole dimension '1'. According to the diagonal reading of the table, as we find the 0 value in the corner, it has to tell us the value of the whole value of the dimension. As we are in the line of the fractal dimension 1, and as we find in it a travel we told its whole value is 1 in 'Mandelbrot fractal dimensions to the rescue', all is coherent. Since we speak, here, of fractal trajectory, the one that illustrates this square is self-similar in all its scales: a helix in helix in helix.

The 3rd line corresponds to fractal dimensions with 2 for whole part.
These dimensions are specially convenient for the measurement of internal deformations.

- in its 1st square we find the state of 'what is used to make the measurement': they are surfaces as we saw in our analysis of strange attractors [to see this again]. According to the diagonal reading this square has to bring the decimal value of the dimension: it's the curvature of this surface that bears this value. Then, for fractal dimension '0', this decimal value was made with only one value, for the fractal dimension '1' the decimal value was made by the combination of two values, and for fractal dimension '2' we see now this decimal value need the combination of 3 values: the two dimensions needed to make a surface, plus the value of the deformation of this surface.

We can understand as follows that the unit of measurement of this dimension is a surface:

We have to measure the deformation of a body on itself, and this needs that all the points of the body permanently coordinate together to exchange their respective places. In effect, during all the deformation two points must never occupy the same place, for this would let empty places, holes in the deserted areas, and would make excessive density in the over-occupied areas.

Then, every point follows its one way, what corresponds to a '1' dimension, and is involved in the same time in the density dimension of the body so that this density remains constant. It happens that a density dimension is a contrast dimension, then a '0' dimension.

Every point is then subjected to the simultaneous effect of 2 dimensions of a different type: one is a '1' dimension, and the other is a '0' dimension.
When a point is subjected to the coordination of 2 similar dimensions, this dimension can be summarized in one dimension only of '1' type as we saw for the previous line of the table, but when a point is subjected to 2 dimensions of a different kind, then they cannot combine and the evolution of the point has to be simultaneously depicted by these 2 dimensions.

Two dimensions, then it makes a surface.
A '2' fractal dimension is then used to describe the evolution of this surface.

          - in the 2nd square of this dimension, we find the dynamic of the evolution of this surface. We saw it's a 'strange attractor', self-similar in all scales [to see this    again]. The position of this square in the diagonal reading of the table corresponds to the synchronization in all scales, what is coherent with the dynamic of a strange attractor.
         - in the 3rd square we find that this dimension manifests itself by statistical values, not by continuous values. Every point is made by the crossing of the '0' dimension and the '1' dimension which apply in the same time to construct the surface described in the 1st square. These crossings cannot be continuously linked one to the other, for this would mean that these 2 dimensions '0' and '1' have found a dimension of common coordination, what is impossible, or what would take back to the fractal dimension of the previous line. This square has to bear the value of the whole number of the fractal dimension: every point is the crossing of 2 separate lines, what is well corresponding to the '2' value of this dimension. We said this dimension is used to measure the phenomena linked to the nuclear force of coherence of matter, for matter particles are fundamentally bodies deforming on themselves [to see this    again].
         - in the 4th square, we have the way the dimension appears. What appears is a body deforming on itself by the coordinate change of position of all its points. In the diagonal reading of the table, this square is that of complex dimension. I don't know well enough the mathematic of complex numbers to find the meaning of this square.

The 4th and last line corresponds to fractal dimensions with 3 for whole part.
These dimensions are the usual dimensions of space-time.

       - in its 1st square we find the state of 'what is used to make the measurement': it's a space volume. As it contains the 3 dimensions seen in previous lines, it has to have 3 distinctive curves to correspond to the crossing of 3 dimensions of a different kind and impossible to combine. This square being that of the self-similarity dimension, in the diagonal direction as well in the vertical direction of reading of the table, its curves have to be self-similar: then they have to be straight lines, to have the same origin, and to have the same unit of measurement.
       - in the 2nd square, we have the dynamic of this 3 D frame. This dynamic consists in the permanent repositioning of all the points at the same place relative to the point used as the origin. The resulting absence of movement does not result from a real absence of movement, but from the complex coordination of the movements in the 3 directions of space, so that these movements permanently neutralize each other. As the resulting fixity is made by the coordination in 3 distinct dimensions, '3' is the fractal value in this square.
         - in the 3rd square, we find the complex dimension of the measurement. The essence of this measurement is that we make it 'from one point toward another', that is: we measure the position of every point relative to the origin.

If we go up all the 3rd column, we see that this measurement is made increasing every time the number of dimensions of the 'instrument of measurement':
- in the '3' dimension, we measure using points,
- in the '2' dimension, just above, the measurement is with the crossing of two lines,
- in the '1' dimension, above the '2' dimension, we represent it with vectors in all the directions of space, but the value of theses vector is finally expressed by the surface joining all their ends,
- and in the '0' dimension, we have to compare an entire volume to another, to measure the ratio between them. The proportion between two surfaces or between two lengths is only a special case where 1 or 2 dimensions are null.

Then, if we go down this 3rd column, the instrument of measurement transforms itself in the following way: volumes, surfaces, lines, points.

The same evolution by the increase each step of one dimension, is also present in the diagrams of the other columns.
- in the 1st column, that of the 'unit of the measurement', we begin with a point in fractal dimension '1', then we have a line, then a surface, and finally a volume.
- in the 2nd column, that of the dynamic of the unit of measurement, we begin with a fixed point in the '3' dimension, then we have dimension '0' and the dynamic of a continuous travel (we know that the table indefinitely continues by putting the previous lines to follow it), then we have dimension '1' and the coordination of 2 dimensions that has the value of a surface, and finally with the '2' dimension we find the strange attractor: in the example of the dripping tap we saw that such an attractor can be made gathering 3 coordinates.
By the way, this means that a strange attractor is a diagram that has the value of a volume, and which elementary unit is a surface.
- the 4th column shows how the dimension finally appears in the way of the observed phenomenon. We also find in it a line to line progress, but this time this progress is more abstract for we find the essence of the dimensions 'according to universe'. This notion of 'dimensions according to universe' [2nd column, prior the 4 columns as such, of the table] refers to the 4 successive stages that all natural phenomenons pass through, as described in a summarized manner in chapter 1.2 of the 1st part (presentation of the hypothesis) of the essay 'Waiting the Higgs Boson' [to see this in the French site]. The essence of these 'dimensions according to universe' is that they are not only made with the combination of an always growing number of dimensions: at its birth every dimension makes a true mutation that radically differentiates it from the others. We will see that the value of fractal dimensions correspond to the value of the 'dimensions according to universe' that 'make the same thing', which is remarkable for every square of the table of fractal dimensions is shifted by one dimension if we compare them to the table of the dimensions according to universe (summarized in the left of the table).

In this 4th column:

- the fractal dimension '0' measures a density of mutation. For example, this dimension can measure the proportion in which a solid metamorphoses into liquid, what corresponds to the ultimate 0 dimension according to universe, the dimension we have defined as that of 'separated points' [chapter 2-4, at the 4th stage in the cycle of matter formation - to see this in the French site].

- the fractal dimension '1' corresponds to a motion that makes a point go all the directions of space, and possibly without ever reaching one of its previous positions. For example, when it has the maximum value 1.99999999... this dimension measures the complete dispersion of a gas in a room by the mean of the Brownian movement of its molecules [last sketch, chapter 11, and chapter 2-5, at the 5th stage in the cycle of matter formation - to see this in the French site]. This fractal dimension is equivalent to the '1' dimension according to universe, that is the dimension we name 'of classification', classification that reach its peak in the spiral or helix-in-helix organisation succeeding in regulating the dispersion in space on all scales in the same manner [chapter 2-8, at the 8th stage in the cycle of matter formation - to see this in the French site].

- the fractal dimension '2' corresponds to the internal deformation of a body. It's equivalent to the '2' dimension according to universe, the dimension that the movement in closed loops [chapters 2-10 and 2-11, at the 10th and 11th stages in the cycle of matter formation - to see this in the French site]. Then, dimension according to universe makes exactly the same thing that corresponding fractal dimension.

- the fractal dimension '3' corresponds to the usual space-time. We still have to see in its 4th square how it appears to us.

- in this 4th square, we find again traditional space-time.
We don't need to make innovations, we only use the tradition: a point makes a line when moving, that makes a plane when moving, that makes a volume when moving. In the diagonal direction, this square corresponds to the decimal value of this dimension: this decimal value depends on the relative speed of these 3 movements.
We remark that the space-time we get by the construction of a line, then of a surface, then of a volume, will not change when using another of the 3 axes to start our construction: the order of the 3 movements that generates the volume is interchangeable. Then, the 3 dimensions are similar, and they are similar in all scales. In its meaning of 'dimension according to universe' [to see above what this expression means], the '3' dimension is also equivalent to the interference of the first 3 dimensions.
At last we find in the meaning of the '3' fractal dimensions, the reconciliation of the first 3 fractal dimensions: they finally find the way to combine together so that we cannot differentiate the 3 axis of space, that we cannot specially give to one or to the other the '0' dimension, or the '1' dimension, or the '2' dimension.

At the end of all these reflections, the traditional concept of measurement of space with 3 graduated orthogonal axis, appears to be a method within four radically different methods to measure the phenomena: four methods that are complementary the ones for the others, and that are all contained the ones in the others.
What we finally discover is that a dimension is nothing but one of the 4 ways we have to combine 4 dimensions, nothing but one of the 4 ways we have to permute their complementary roles.

The interest of this table could be to help find the possible 'nonprobability' measurement of the fractal dimension '2'.

Generally, the idea would be to think how every dimension is the 'derivative' of the just above dimension, and the 'primitive' of the just below dimension.
The handling of the derivatives by Newton and Leibniz was the mathematic tool that made possible all the development of the scientific calculation since the XVII century.
Today, we still consider that a derivative is the instantaneous change of the direction of a curve: it would be the limit of this change when time duration tends to zero. This concept is effective, but it is not convenient to think that a change can really be made in zero time: in zero time a change can only be zero.
As our hypothesis proposes that dimensions are fundamentally only deformations, it does not have this abnormality: we consider a travel as the coordination of 2 deformations, and we can very well stop one of the deformation making it zero, and then measuring the other deformation that has not to be specially zero at the same time. In our hypothesis we call 'derivative' of a curve, the value of one of the deformations of a travel, when its combined dimension is zero.

The dynamic of the '2' deformation has a 'volumetric' aspect that provokes its statistical feature, for we cannot calculate the edge of a parallelepiped if we only know its volume.
I hope
the analysis of this table will enables somebody to find the evolution of the surface of one of the sides of this parallelepiped, finding by this way the absolute length of its edges.

Last update of this page: 09 mai 2010

home

Math

top

author