home

contents Mathematics

previous :    how to travel from one number toward another?

next :    the difference between fractal and space dimensions

After this wide detour to learn how to calculate decimal values correctly, we go back to curved deformations.
We left them [to see again    this moment] saying that in a single point we wanted to represent the whole set of solicitations which tend to make that point move in space. And we have acknowledged then that these solicitations have to be represented by an infinite number of vectors, each of these vectors having a specific intensity, and each being oriented in a specific direction of space.
To represent the whole set of vectors which compel the body to move, we must have at our disposal 3 distinct types of data:
       1/  first, we have to indicate that what occurs to the physical body, is a deformation of its position, that is, a move in space. It could have been a different type of deformation. For example, it could have been a deformation which pierces it, or stretches it, or inflates it, or compresses it.
       2/  then, we have to indicate the intensity of the deformation of its position.
       3/  at last, we have to know how this intensity varies, along with all the directions of space.
 

Now, it happens that our analysis of the generation of whole and decimal numbers, shows us that a fractional number necessarily holds 3 types of distinct data:
       1/  the first concerns the whole number it is linked to.
       2/  the second concerns the sequential ordering of the deformations made to the unit.
       3/  the last, concerns the value of this deformation for each of the decimal sequences.
 
 
 

So, this suggests a simple way to measure the dimension of curved deformation to which a point is subjected: we only have to use an irrational number whose whole part would tell the type of deformation, and its decimal part -- whose length is infinite --  would tell how the intensity of the deformation varies for every of the infinite number of space directions. At this point, we remember the fractal dimensions of Mandelbrot. And we wonder: isn't it exactly what they do and describe? Don't they precisely tell how a phenomenon deforms itself, and how that deformation varies according to space directions?

First, we consider the whole digit they bear before the decimal point.

       - 0 -  we began introducing deformation dimensions with the deformations of a contrast, such as a 'Cantor dust': that is a bar whose central 1/3 is removed, whose central 1/3 of the 2 remaining segments is removed, and so on, to infinity [to see      that figure again]. It happens that the fractal dimension of such a Cantor-dust, where the deformation implies no displacement, is Log 3/ Log 2, that is about .63.
Then, its whole part is 0.

       - 1 -  as we shall see in the next examples [images below] the fractal values of the paths that Mandelbrot gives in his book 'The Fractal Geometry of Nature', all have values between 1 and 2. That is to say that their whole part is always 1.

       - 2 -  at last, the fractal value of a 'Peano curve', which deforms the pavement of a surface on itself, is 2 [see this figure     in the next page]. The basis of that figure is to regularly change the distribution of white part and black part on a sheet without changing their mutual proportion: every time, it makes a more tortuous division between the 2 surfaces.
Then, the whole value 2, in a fractal dimension, may have to do with the deformation of a body on itself.
 
 

Now, the decimal value of fractal dimensions: we know that most of the time it's an irrational number, resulting from the division of 2 logarithms. Then, it does hold infinity of sequenced deformations.
 
 

What remains to be seen, is the graph representation of that dimension.
[the images are from the french translation of the book of Benoit Mandelbrot: 'Les Objets Fractals' - Flammarion publisher]
For example, Mandelbrot gives the fractal dimension Log 4/ Log 3, that is roughly 1.2618, for the Von Koch 'snowflake curve'. This curve cannot really be drawn, for it corresponds to an infinite process: we begin with an equilateral triangle, on every side of the triangle, we make an equilateral triangle on its central 1/3, on every side of the last triangles we made, we make an equilateral triangle on their central 1/3, and so on, . . . till infinity.

 

generation of the Von Kock 'snowflake curve' (to go on till infinity)

the Von Kock 'snowflake curve' Dimension = Log 34 ~ 1,2318

 

Another example: for a fractal dimension value Log 5 / Log 4, that is roughly 1.16, we get this kind of curve, which we also have to carry on to infinity. Here, only the first 2 steps are represented.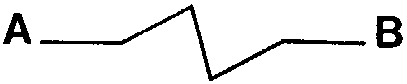

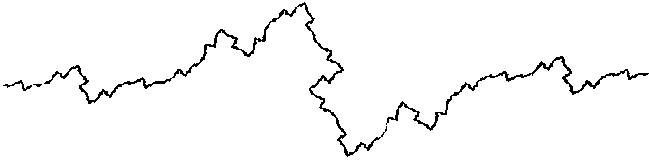Dimension = Log 45 ~ 1,16

 
 

We immediately notice the graph significance, of the correspondence between fractal dimensions and such curves.
To represent the value of a force of a vectorial type, a vector precisely was enough.
A fractal curve is not far from having the same simplicity as a vector, for we needn't represent the whole infinite curve. As we find the same curve on all scales, and the same details in all details, we have no need to bother drawing it all. One only scale is enough. And we have better use the bigger one. Thus, in the case of the dimension 'roughly 1.16', the diagram AB is enough to virtually represent the infinite number of curves which are made on the same model, on all possible scales.
Nevertheless, a question remains: in the same way as we can graphically calculate the combination of several vectorial forces by using their resultant vectors, can we hope to calculate graphically the combination of several curved deformations with any construction made on their fractal curves?
We shall make no suggestion here about this issue which will remain open.
 
 
 
 
 
 

How to find a fixed value, for the fractal dimension of a path
 

Now, if we consider the curve AB in the above drawing, not as a drawn figure, but as the path of a body moving from A to B, we say to ourselves that this type of path calls well enough to mind what occurs when a body is driven toward another by a curved deformation: the graph shows that it starts from A, arrives in B, and that to make this path it isn't subjected to an attraction directed toward B only, but also toward other directions.
In short, it ends up arriving in B and not missing it, only because these attractions, according to all different directions, are well combined together. And this, on all scales of the path.
Nevertheless, there is a major objection, made by Mandelbrot himself, concerning the use of fractal curves as the valid representation of a path followed by a moving body. This objection concerns the length of the path.
 

In fact, if we calculate the length of a fractal curve, we notice it can be infinite. Every time we go down one notch in the scale details of its path, we turn a straight segment into a series of segments that undulate on this 1st segment. As a straight line is the shortest way between 2 points, therefore every step in the 'refinement of detail' has for consequence to lengthen the curve. Some infinite suites converge to a finite sum, but not in this case, for the lengthening factor of the path does not decrease with the scale of details.
Thus, if the curve is of infinite length, we cannot use it to measure the path of a body, which will be, for its part, perfectly finite.
We can also decide not to draw the curve in all its infinite details, in order to have a fixed result. But in this case, according to the scale used to measure the path, that is according to the degree of details used, the length of the path will not be the same every time.
 
 

So, a fractal path has an infinite length, or has a variable length according to the scale of its measurement. Therefore, we start off pretty badly when using a fractal curve to represent the path of a body driven by a curved deformation. On this point again, the analysis we have made on decimal numbers, will be useful to understand where the anomaly comes from.

We remember that we have said that a fractional number holds 3 data, and thus is equivalent to a 3 D space, that is a volume. And here, we only want the length of a path, which is a 1 D datum.
If for instance, we have a problem which says, 'the volume of a parallelepipedic body is 1.26 m3, what is its length?', we know that we cannot solve it. It's right, that the value 1.26 was obtained by multiplying a length with a width and a height. But conversely, we cannot find again these 3 data which, nevertheless, are 'contained' in the volume value. To find the length, we first have to 'deflate' the volume by giving the height, then to 'de-flatten' the result by giving the width.
In the same way, to calculate the length of a fractal path, before the calculation we have to give the 2 data that fractal dimension has 'mixed' with the path length: the straight line dimension between the 2 extreme points of the path, and the scale of details on which the path is made, chosen among the infinite number of possible scales.
The anomaly of the infinite length of a fractal curve only comes from the fact that we want to use 'all' the fractal dimension to calculate the length of a path, whereas a fractal dimension bears 'too much' data for this. We have to 'deflate' it to find out the length it contains.
On that aspect of the fractal dimensions we diverge from the presentation of Mandelbrot. To the question: 'how long is the coastline of Brittany?', Mandelbrot answers: it has an infinite length, for we always can follow it on a tinier scale. The journey may be done in a car, or by a pedestrian, or by a mouse, or it can go round all its sand grains, or it can go round all the atoms that mark its limit: each time the path will be longer and will get closer to infinity. To the same question here we answer: the Breton coastline always has a fixed length, but it has an infinite number of lengths, every one of them corresponding to a scale of measurement among the infinite number of possible scales.
 
 

In a system of measurement with coordinates, a path has only one possible length. In a system of measurement with deformation dimensions, a path has an infinite number of possible lengths, that are summaries in one number only. Then, a fractal dimension is infinitely bigger in data than a coordinate dimension. It only asks, which of the paths we are to take, before giving us its length.

 

home

Math

top

next :      the difference between fractal and space dimensions

author