home

contents Mathematics

previous :   'in theory' the dimension of a contrast can be self-similar

next :   counting in a different way

The trap in the vectorial representation of the forces

Then, by nature, the value of the deformation doesn't move on a straight line toward infinity, but moves round and round the closed curve 0/1. Often, to remind this propriety, we will speak about 'curved' dimensions of deformation, by opposition to coordinates which are 'straight' dimensions for we measure them on straight axes.

We saw how we can describe the evolution of a contrast with 'curved' dimensions. We will now see how they also can measure travel paths. The key point is that we have to clearly differentiate the 'curve' followed by a point, and the 'curved' value that makes it move.
In effect, what we will try to track, is not the path in itself, which will be only a result of the deformation dimension, but the organization of the forces which apply on a point and make it move.
 
 

Fundamentally, that dimension will be useful to describe a force field, for instance an electromagnetic field. Usually, such a field is described by a set of vectors, which indicate for example, in every point, the direction and the velocity of a flow. Which fits with coordinate dimensions (opposite: an example of a force field). [picture from an article of G. Hooft : les théories de jauge et les particules élémentaires - Pour la Science]

The originality of our approach, is in not adding in each space point, the whole set of the promptings which drive it, and in no 'reducing' it in a single vector. We suggest that we let open, 'not solved', the combination of these promptings. So, in the general case, infinity of vectors exists in every point. Each indicates in its specific direction, the intensity of the prompting of the phenomenon in a point.

For example, in the case of 2 electric charges of an opposite sign, the force field is represented by various curves joining the two charges. The representation with vectors in a system of coordinates, summarizes the effect of this field by 2 vectors pointing from one charge toward the center of the other: they attract one another, and the 2 vectors describe the intensity and the direction of that attraction.
 

usually, the attraction between 2 electric charges is summerized with 2 vectors

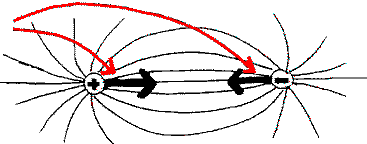In our system of representation we will not 'summarize' the effect of the electric field, but on the contrary we will let it spread in all the directions of space. Every field line, corresponds to an effect, a prompting toward the other charge. And we represent, for every line, the direction of that prompting (tangential to the curve) and its intensity (the more it is pointed toward the other, the bigger the intensity).
We point out, that if the 2 charges are weak, or if both are strong, the drawing will look the same, and will infer one from the other by homothetie. In short, they will be self-similar.
 

our proposal to represent the same electric attraction

This representation, looks a bit like a heart filled with vectors, whose intensity varies between a minimum and a maximum. That's the first 'curved aspect' of the value for it go round a circle from 0/1 to 1/0.
And the resultant of all these vectors, if you calculate it, would be a unique vector which would describe the direction and the velocity of the curve that the charge follows. That's the second 'curved aspect' of that dimension.
 

It may appear, at first, that we are complicating things by no reducing the set of the promptings in a point with a single vector.
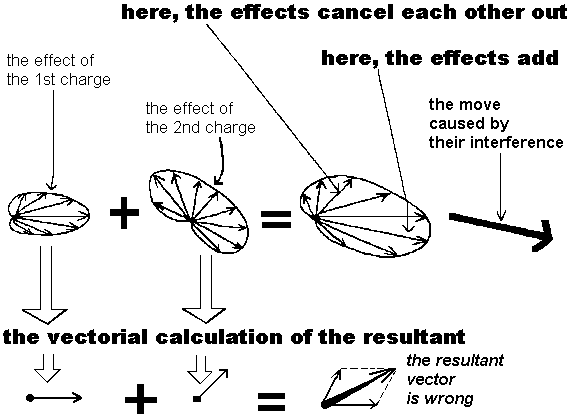
But if we take a point which is not only prompted by a unique charge, but which is prompted by 2 charges or more, we will then have the following case: every charge causes a curve dimension of deformation and they all gather at the same point. A concordance or opposition of their respective shape can occur between the 2 dimensions. This concordance or opposition, will show how the effects of the dimensions add in some directions, or cancel each other out in other directions. A single vector for each charge would have completely erased these data that may be basic to understand the phenomenon and its evolution.

So, thanks to the device consisting in keeping the whole set of the promptings in a point   instead of reducing it to a single vector   we keep a representation of the phenomenon that behaves in a way similar to the phenomenon itself. That's then the way to help the understanding of the phenomenon, not the way to complicate it. In the reverse, the seeming simplification of vector analysis sometimes lead to completely wrong results, and this can occur every time a phenomenon depends on the interference of several causes which varies with their directions. [to see    a specially important consequence of this analysis]

In addition, we shall see that the representation of an infinite number of intensity, in an infinite number of directions . . . is not so complicated. It might almost be as simple as the representation with a single vector.
But before being able to see that point, we have to make a mathematical detour toward numbers.
Because, if we have said that it is the representation with coordinates which handicaps our understanding of some phenomenon, we must now prove that it is our conception of numbers and the way we calculate them which handicap our understanding of the dimensions.
 
 
 

home

Math

top

next :   counting in a different way

author