home
contents Mathematics
the measurement of the deformation of a contrast
home |
contents Mathematics |
next
: the measurement of the deformation of a contrast |
| direct to all other pages of the section ----> | 00 | 01 | 02 | 03 | 10 | 11 | 12 | 20 | 21 | 30 | 31 | 32 | 33 | 34 |
What is a dimension?
|
The key notion developed here, is that numbers not always have one unique
dimension: a number such as '2' can as well be the measurement of a
length, than the measurement of a surface or the measurement of a volume.
This does not only mean that you can put a 'm', 'm2' or 'm3' unit behind it, but mainly that according to the number of dimension it bears it must not be calculated in the same way: 2 x 2 will not give the same result if the related '2' have 1, 2, 3 or 4 dimensions. |
Before developing this idea, we make
a short historic of the notion of dimension.
| In the old time, a dimension was either the height, or the length, or the depth of a thing. |  |
 |
In the XVII century,
Descartes gave a more general definition : a dimension is a coordinate
in a set of orthogonal axes. Height, length and distance, became just special
cases of coordinates. Usually these coordinates are said to be that of
Euclidean space.
That definition proved to be specially convenient to describe the mechanical movement of a point in space. |
In the mid XIX, the mathematician
Riemann still gave more generality to the notion of dimension. The physical
phenomena evolving by the prompting of various parameters, since Riemann,
every parameter that prompts in a process has been call a 'degree of freedom',
and every coordinate stands for one of these degrees of freedom. The key
point is that nothing prevents us from giving to each point more than three
space coordinates, however geometry becomes more complicated each time
the number of space dimensions increases.
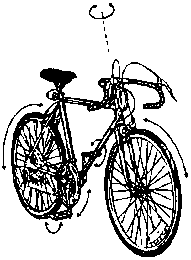
Here is the example given
by Ian Stewart of the dimensions of a motion of a bicycle in his book 'Does
God Play Dice?':
| "A
bicycle has (at a conservative estimate) five main moving parts: the handlebars,
the front wheels, the crank-chain-rear-weel assembly, and two pedals. Each
requires one position coordinate and one velocity coordinate to describe
it: an engineer would say it has 'ten degrees of freedom'. To ride a bicycle,
you must gain intuition about the motion of a point in 10-space! Maybe
that's what makes it so hard to learn."
[Ian Stewart - Does God Play Dice? - Penguin Books 1990] |
 |
| Therefore, a dimension was at first a concrete part of the things, then a dimension became a coordinate of a moving point in a 3 D space, then a coordinate became a degree of freedom in a 'n' dimensions space, 'n' being as big as needed. |
For the other part, the scientists
had to acknowledge that they left aside numerous natural phenomena they
cannot calculate. For example, something as simple and ordinary as this
one: you throw away a cork in a river and you ask where it will be in an
hour. Still in the same place, trapped in a whirlpool? Very far away downstream?
May be upstream, drift by a counter-current? May be on the other bank?
No equation will help you.
Equations can calculate with breathtaking
precision the evolution of a spacecraft lunch in space through the solar
system, but they leave you if you want to predict even approximately the
evolution of a falling leaf, right in front of your nose, jolted in a very
smooth draft.
In the standard scientific jargon,
these phenomena insoluble with equations are called: 'deterministic chaos'.
Deterministic, for real effects that we can precisely spot and measure
determines the future of the events. Chaos, for we know nothing about what's
going on despite our knowledge of all what determine the events.
And deterministic chaos appears
to be common thing in nature. For instance, water flow and air stream are
chaotic in many situations. To have deterministic chaos, you only have
to take 3 body and to find there reciprocal influences. The earth round
the sun, it's perfectly depicted by an equation, but the earth with the
moon and the sun and their respective attractions, already it's fundamentally
unpredictable. We can grasp it by tinker equations with approximations
and corrections which are not very mathematically limpid, but planets do
not go round quickly, and we don't ask what will be in a billion years.
To the question: 'is the solar system stable?', no one can tell you with
certainty.
The usual explanation is to state
that the unpredictability of such phenomenon results of an 'extreme sensibility
to initial conditions'. You throw the cork in the river one part of a millimeter
left or right, and his travel will be completely different, only by the
fact that a very small gap when starting will be magnified during the travel.
As time passes, this gap will increase and increase, and finally the cork
will be brought in a stationary whirl or in a well-formed current which
will rapidly carry it downstream.
It happens that to calculate the
motion we have to round off the result of a calculation before beginning
the next for it never falls 'right'. Whatever the precision, when we round
off it always remains in the result a very tiny gap with the 'right number'.
This small gap grows with each of the calculations, and ends being big
enough to completely distort the evolution result.
| We shall attempt
here to propose a new way of tackle this sort of problem, and to suggest
that the powerlessness to describe with an equation the evolution of a
point's coordinates in a chaotic phenomenon, doesn't stand in real paradoxes
or real unpredictability of phenomena, but simply stands in the inadequacy
of our way to represent them, that is to dimension them.
The point is not that we have a problem without solution, it is that we do not put it correctly, and we do not put it correctly because we put it in terms of coordinate dimensions, that is in terms of paths of points whose coordinates evolve in space. What we will try to show, is that a brand new definition of dimension is needed, more general still than coordinates in a 'n' dimensions space. |
The usual concept is to describe
a dimension as the value we give to a coordinate.
Then, how shall we describe here
a dimension? We state,
that a dimension, is the value we give to a deformation.
By and large, we will speak here
about 'deformation dimensions'.
What is a deformation dimension?
To first define what the essential
link between dimension and deformation is, we shall now demonstrate that
some deformations can be measured without ever using any coordinate.
home |
Math |
top |
next
: |
author |